Introduction to Mathematical Operations
Mathematical operations form the backbone of mathematics, encompassing the various ways in which numbers can be manipulated and analyzed. At their core, these operations—addition, subtraction, multiplication, and division—provide a framework for solving problems, making informed decisions, and understanding the world around us. Each of these operations serves a distinct purpose, yet they all intertwine to enhance our ability to quantify and evaluate different scenarios.
Addition, the operation of combining quantities, allows individuals to determine totals or sums effectively. This operation is crucial not only for basic arithmetic tasks but also plays a vital role in everyday situations, such as budgeting or measuring. Conversely, subtraction aids in understanding differences by providing a method for calculating how much remains when a quantity is removed. This operation is equally significant in various applications, from financial calculations to time management.
Multiplication extends the concept of addition; it enables the determination of cumulative totals across repetitions of the same quantity. Often referred to as scaling, this operation is widespread in fields like physics and engineering, where it can be used to calculate forces, areas, and volumes. Division, on the other hand, serves to partition quantities evenly, allowing for comparisons and resource distribution. This operation is essential in logistics, finance, and many day-to-day activities where resources need to be allocated efficiently.
In summary, understanding mathematical operations is fundamental for both academic success and practical life management. Their application extends beyond pure mathematics into science, finance, and various other fields, underscoring their importance in daily life. By mastering these operations, individuals can enhance their analytical skills and approach problems with greater confidence and competence.
The Four Basic Operations
Mathematics, at its core, is founded on four basic operations: addition, subtraction, multiplication, and division. Each operation serves a distinct purpose and is fundamental in processing numbers, contributing to arithmetic competence.

Addition is the process of combining two or more numbers to arrive at a total. For instance, when you add 2 and 3, the result is 5. In mathematical notation, this is represented as 2 + 3 = 5. Addition is not only integral for simple calculations but also forms the basis for more complex mathematical concepts, such as algebra and calculus.
Subtraction, on the other hand, involves removing one number from another to find the difference. Using the previous example, if you subtract 3 from 5, the operation can be written as 5 – 3 = 2. Subtraction can be seen as the inverse of addition and is crucial in various real-life applications, such as budgeting and inventory management.
Multiplication expands on the concept of addition through repeated summation. For example, multiplying 4 by 3 (4 x 3) results in 12, which is the same as adding 4 three times (4 + 4 + 4 = 12). This operation streamlines calculations and is instrumental in various fields, including geometry and algebra.
Finally, division serves as the process of determining how many times one number is contained within another. For instance, dividing 12 by 4 gives the quotient of 3 (12 ÷ 4 = 3). Division is essential for distributing quantities evenly and is commonly utilized in cooking, financial planning, and even programming.
Each of these operations showcases a foundational block in mathematics, enhancing our ability to perform calculations efficiently. Understanding how to execute and apply these basic operations is crucial for developing mathematical proficiency and navigating everyday numerical challenges.
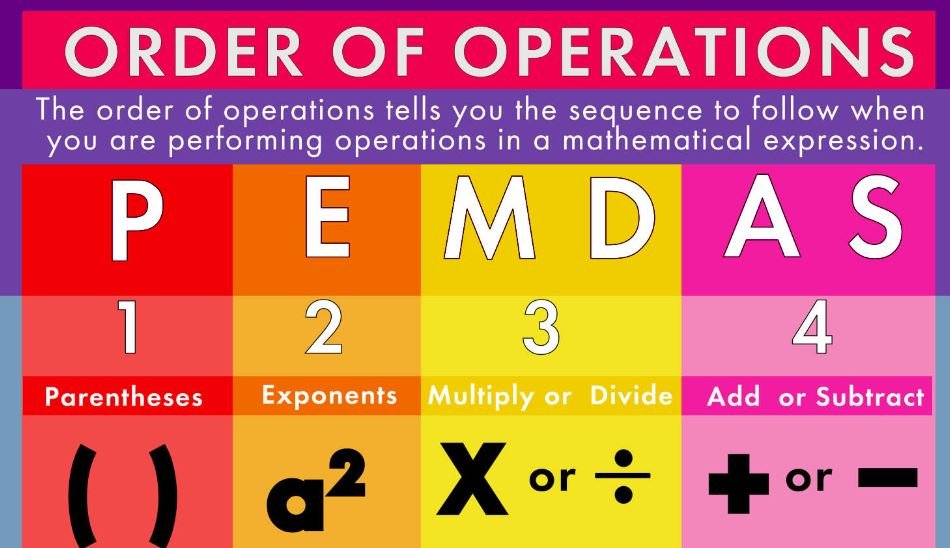
Order of Operations
The order of operations is a fundamental concept in mathematics that dictates the sequence in which different operations should be executed in expressions. This sequence ensures that mathematical expressions are evaluated correctly and consistently. A commonly used mnemonic to remember this order is PEMDAS, which stands for Parentheses, Exponents, Multiplication and Division (left to right), and Addition and Subtraction (left to right). Some regions may prefer the BODMAS acronym, where ‘B’ stands for Brackets, followed by Orders (or Exponents), Division, Multiplication, Addition, and Subtraction. Despite the terminology differences, the underlying rules remain the same.
To apply the order of operations effectively, one should follow a step-by-step approach. Start by solving any expressions enclosed in parentheses or brackets. Next, evaluate any exponents or orders in the equation. Following that, perform any multiplication or division from left to right, and finally address any addition or subtraction, also from left to right. This structured approach prevents ambiguity, ensuring that everyone arrives at the same answer when evaluating a mathematical expression.
For example, consider the expression 8 + 2 × (3² – 1). First, evaluate the expression inside the parentheses: (3² – 1) becomes (9 – 1), equating to 8. Second, the expression now reads 8 + 2 × 8. Next, follow the order of operations to multiply before adding: 2 × 8 equals 16. Lastly, add 8 and 16, resulting in 24. Adhering to the order of operations is crucial, especially when dealing with complex equations, as it significantly impacts the final outcome. Mastery of these rules is essential for any student or individual who wishes to navigate the realm of mathematics confidently.
Advanced Mathematical Operations
Advanced mathematical operations extend the fundamental concepts of arithmetic and algebra, introducing new ways to manipulate and analyze numbers. Among the most significant of these operations are exponentiation, square roots, and logarithms, each serving distinct purposes in mathematical calculations and applications.
Exponentiation is the operation of raising a number, known as the base, to a certain power, represented by an exponent. For instance, in the expression 23, the base 2 is multiplied by itself three times, resulting in 8. Exponentiation not only simplifies the representation of large numbers but is also foundational in various mathematical areas, including calculus, financial modeling, and algorithm complexity.
Square roots, denoted by the radical symbol (√), represent the inverse operation of squaring a number. For example, the square root of 16 is 4, as 42 equals 16. Square roots are particularly useful in geometry, where they help in calculating the lengths of sides in right-angled triangles, thanks to the Pythagorean theorem. Additionally, square roots play a significant role in statistics, particularly in the calculation of standard deviations.
Logarithms, on the other hand, provide a method for solving exponential equations. The logarithm of a number is the exponent to which the base must be raised to yield that number. For example, log2(8) equals 3 because 2 raised to the power of 3 equals 8. Logarithms are crucial in various fields, including computer science, where they assist in analyzing algorithms’ time complexity, and in finance, where they help in modeling exponential growth and decay.
In conclusion, understanding advanced mathematical operations like exponentiation, square roots, and logarithms is essential for tackling more complex mathematical challenges. Their applications span diverse domains, influencing fields as varied as engineering, physics, finance, and data science, underscoring their importance in both theoretical and practical contexts.
Operations with Negative Numbers and Fractions
Mathematical operations involving negative numbers and fractions can often pose challenges to learners. Understanding how to effectively perform these operations is crucial for solving various mathematical problems. The foundational rules governing the manipulation of negative numbers and fractions will be discussed here, incorporating clear examples for better comprehension.
When adding or subtracting negative numbers, it is essential to recognize that adding a negative number is equivalent to subtraction. For instance, to calculate (3 + (-5)), one would simplify this as (3 – 5), resulting in (-2). On the other hand, subtracting a negative number translates to addition. Thus, (7 – (-2)) becomes (7 + 2), which equals (9). This understanding allows for clearer navigation through problems involving negative numerals.
Fractions also introduce their own set of rules when interacting with both negative numbers and other fractions. For example, when multiplying a fraction by a negative number, the result inherits the negative sign. Taking the calculation (-2 times frac{3}{4}) yields (-frac{6}{4}) or simplified to (-frac{3}{2}). Similarly, division follows this pattern; (-frac{3}{4} div 2) results in (-frac{3}{8}).
Furthermore, adding and subtracting fractions requires a common denominator. For instance, to add (-frac{1}{2}) and (frac{1}{4}), convert (-frac{1}{2}) to (-frac{2}{4}). The operation then becomes (-frac{2}{4} + frac{1}{4} = -frac{1}{4}). These conventions are essential in maintaining accuracy while executing mathematical operations. Through understanding these principles, learners can confidently tackle calculations involving negative numbers and fractions.
Applications of Mathematical Operations in Real Life
Mathematical operations are not merely abstract concepts confined to textbooks; they permeate our everyday lives and are foundational in various fields. From engineering to finance and statistics, the application of mathematical operations plays a crucial role in decision-making and problem-solving.
In engineering, for instance, mathematical operations are essential for designing structures and systems. Engineers routinely perform calculations to determine load capacities, material strengths, and the dimensions of components. For example, when constructing a bridge, civil engineers use arithmetic and algebraic operations to compute the required materials that can withstand expected loads and environmental conditions. These calculations ensure safety and functionality, underscoring the necessity of a solid grasp of mathematical operations.
In the realm of finance, mathematical operations are fundamental in management and forecasting. Budgeting demands addition and subtraction to track expenses and revenues, while multiplication and division are critical for calculating profit margins and return on investments. Additionally, in financial modeling, statistical operations are leveraged to analyze trends, allowing businesses to make informed decisions based on historical data. The ability to interpret these operations enables organizations to allocate resources more effectively and optimize financial performance.
Statistics is another field where mathematical operations are indispensable. The extraction of meaningful information from data relies on the competency in statistical calculations such as averages, percentages, and standard deviations. For example, health researchers use these operations to analyze data from clinical trials, determining the efficacy of new drugs or treatments. Understanding how to manipulate data through mathematical operations is vital for drawing conclusions and making predictions based on empirical evidence.
Overall, the integration of mathematical operations into various disciplines illustrates their practical utility and the necessity of mastering these skills in both professional and personal contexts. The real-world examples provided demonstrate that a comprehensive understanding of mathematical operations is not only beneficial but essential for success across multiple domains.
Common Mistakes in Mathematical Operations
Mathematical operations are foundational skills necessary for a broad range of academic and real-world applications. However, when applying these operations—whether addition, subtraction, multiplication, or division—individuals often encounter common mistakes that can lead to inaccurate results. Recognizing these pitfalls is crucial for improving mathematical practice. One prevalent error is misplacing decimal points, which can drastically alter the outcome of calculations. For instance, writing 0.5 instead of 5 can represent a significant difference in both theoretical and practical scenarios.
Another frequent mistake occurs in the order of operations. Many learners forget the established sequence that dictates that multiplication and division should be carried out before addition and subtraction. This oversight can result in incorrect answers and a misunderstanding of fundamental algebraic principles. A useful strategy to avoid such mistakes is to employ mnemonics, like PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction), which aids in recalling the proper order of operations.
Additionally, arithmetic errors such as neglecting to carry a one in addition or miscalculating a multiplication product come into play for students and professionals alike. These mistakes often stem from simple lapses in attention or from underestimating the complexity of the operation being performed. To mitigate these issues, it is advisable to develop a habit of reviewing calculations thoroughly. Double-checking work not only helps identify mistakes but also strengthens mathematical understanding and retention.
Moreover, reliance on calculators without a fundamental grasp of arithmetic can lead to errors, especially when interpreting the results. It is advisable for individuals to sharpen their basic skills and engage in mental calculations where possible. This combination of awareness, review, and skill enhancement can significantly diminish mistakes in mathematical operations, ensuring increased accuracy and confidence in one’s mathematical abilities.
Tips and Tricks for Mastering Mathematical Operations
Enhancing speed and accuracy in mathematical operations is a goal for many students and professionals alike. Mastery of fundamental skills can significantly improve efficiency and confidence when approaching complex calculations. One effective strategy involves mental math, which allows individuals to perform computations without the aid of calculators or paper. To develop mental math skills, one should practice basic addition, subtraction, multiplication, and division facts until they become second nature. For example, consistently working with numbers close to multiples of ten can simplify many operations, making it easier to derive solutions quickly.
Another useful method is the incorporation of visual aids. Techniques such as drawing number lines, pie charts, or utilizing manipulatives can provide a clearer understanding of mathematical concepts. Visual representations are particularly beneficial in comprehending operations such as fractions and ratios, where spatial relationships are crucial. For instance, when adding fractions, illustrating the problem using pie charts can help students see how different fractions combine visually.
Additionally, practicing estimation enhances one’s ability to approximate answers, which can be immensely useful in verifying the plausibility of results. Techniques such as rounding numbers to the nearest whole or significant digit can provide a quick way to calculate an answer’s reasonableness during more complex calculations. This method not only saves time but can also reduce errors that result from overly complicated arithmetic.
Lastly, engaging in regular practice through puzzles, math games, and flashcards can make the mastery of mathematical operations enjoyable. These activities often incorporate repetition in a fun environment, reinforcing skills and concepts. By integrating these strategies into daily routines, individuals can significantly improve their mathematical capabilities, leading to better performance in both academic and professional settings.
Mastering mathematical operations is a fundamental skill that underpins much of our everyday problem-solving, decision-making, and analytical reasoning. Throughout this guide, we have explored various mathematical operations, including addition, subtraction, multiplication, and division. Each of these operations serves as a building block for more complex mathematical concepts. By gaining a thorough understanding of these basic operations, individuals can enhance their overall mathematical proficiency.
It is important to recognize that mathematical operations are not merely abstract concepts but are integral to navigating real-world situations. Whether budgeting finances, measuring distances, or calculating time, the application of these operations is omnipresent. Furthermore, proficiency in mathematical operations contributes to logical thinking and the ability to draw conclusions based on data analysis, skills that are essential in many professional fields.
Regular practice is key to maintaining and improving one’s mathematical abilities. Engaging with mathematical problems on a consistent basis can lead to greater confidence and a stronger grasp of concepts. Utilizing resources such as online platforms, workbooks, or study groups can significantly enhance one’s practical understanding of mathematical operations. As learners challenge themselves with diverse problems, they not only reinforce their existing knowledge but also discover new methods and techniques for problem-solving.
In our increasingly data-driven world, the ability to perform mathematical operations with ease is invaluable. As you continue your journey in mastering these skills, remember that persistence and practice are essential components of success. By committing to refining your mathematical abilities, you are equipping yourself with essential tools that will serve you well in various aspects of life, both personal and professional.